π/2 9 cos2(θ) dθ 0 494405-Evaluate the integral. π/2 9 cos 2(θ) dθ 0

Uploaded By johnnyme07 Pages 4 This preview shows page 2 4 out of 4 pages π 2, 7 π 4 Solving (r 2 = sin 2 θ90°) trig If sinθ>0 and tangθ math given sinθ=5/13 and π trig cosθ =5/13 with π/2 θ trignonmetry 6 Prove that tan λ cos^2 λ sin^2λ/sin λ13/04/19 · # π/2 0 (1 2 cos2 θ cos2 2 θ)dθ = 4 R2m l · 3π 4 = 3πR2m l Created Date 4/13/19 PM

Solutions Manual For First Course In Differential Equations With Modeling Applications 11th Edition By Mankiw234 Issuu

Evaluate the integral. π/2 9 cos 2(θ) dθ 0

Evaluate the integral. π/2 9 cos 2(θ) dθ 0-Use a graphing utility to graph three solutions, one of which passes through the given point ds/dθ = tan 2θ, (0, 2)27/04/18 · Using the double angle formula we massage this into forms #cos theta = cos a# and get #theta = \pm 1^circ 360^circ k or theta = 180^circ 360^circ k #

Polar Curves Intersections Ppt Download

21/09/11 · Properties of Beta Function(1) B(m, n) = B(n, m) π 2(2) B(m, n) = 2 sin2m−1 θ cos2n−1 θ dθ 0 ∞ xm−1(3) B(m, n) = dx 0 (1 x)mn 1 xm−1 xn−1(4) B(m, n) = dx 0 (1 x)mn N B Vyas Beta & Gamma functions0 cos2 θ dθ = 0 1 2 (1 cos 2θ) dθ halfangle identity 1 £ 1 ¤π/2 £¡ ¢ ¤ = 2 θ 2 sin 2θ 0 = 12 π2 0 − (0 0) = π 4 Rπ Rπ£ ¤2 Rπ£ ¤2 Rπ 9 0 sin4 (3t) dt = 0 sin2 (3t) dt = 0 12 (1 − cos 6t) dt = 14 0 (1 − 2 cos 6t cos2 6t) dt Rπ£ ¤ Rπ¡ ¢ = 14 0 1 − 2 cos 6t 12 (1 cos 12t) dt = 14 0 32 − 2 cos 6t 12 cos 12t dt £ ¤π £¡ ¢ ¤ = 14 32 tΠ 2 7π 4 solving r 2 sin 2 θ r 2 cos2 θ for x π School National Chiao Tung University;

09/12/ · Trigonometric Identities (1) Conditional trigonometrical identities We have certain trigonometric identities Like sin2 θ cos2 θ = 1 and 1 tan2 θ = sec2 θ etc Such identities are identities in the sense that they hold for all value of the angles which satisfy the given condition among them and they are called27 π 2 sen3 θdθv 9 π 2 senθ sen2 θdθ v 9 π 2 senθ 1 cos2 θ dθ v 9 π 2 senθ from IT 101 WORD 1 at University of Technology and Life Sciences inThus adding both, we get 2I = ∫cos²θ (dθ) in limits (0 to π/2) ∫sin²θ (dθ) in limits (0 to π/2) = = ∫{cos²θ sin²θ} (dθ) in limits (0 to π/2

24/07/14 · Solución Por simetría A = 2 ⋅ ∫0 π 1 2 r2 dθ = ∫0 π 2 cos θ 2 dθ A = ∫0 π 4 4cos θ cos2 θ dθ A = ∫0 π 4 4cos θ 1 cos 2θ 2 dθ A = 1 2 ∫0 π 8 8cos θ 1 cos 2θ dθ A = 1 2 ∫0 π 9 8cos θ cos 2θ dθ = 9π 2 Área en coordenadas polaresFor ∫cos2 3θdθ For a correct integral expression including limits θ π 2 1 2 jw =1 , arg jw =3 B1 B1 ft B1B1 ft B2 6 w* and jw in correct positions relative to their w in first quadrant Give B1 for at least two points in correct quadrants (ii) (1 )(1 *) 1 e e ( e )( e 3j) 2 3j 1 2 3j 1 2 3j1 2 w w = θ − θ θ − θ 4 1 2 1 2 =1 1 (cos −jsin3θ ) 5 cos3θ 4 = M1 A1 M112/01/19 · 1 cos2 θ = π 0π cos2 θdθ = π 1 π 0 (1/2)dθ 1 2 = Because sin2 θ cos2 θ = 1, and the integrals of sin2 and cos2 are equal (over suitable intervals), one can replace them by 1/2

Problem 1 Think Of A Cone 45degrees Is Cut With A Horizontal

Math Polar Coordinates Ppt Download

11/02/15 · Evaluate the integral sin^7 θ cos^5 θ dθ 0, pi/2?4 Abstract and Applied Analysis In this study, our goal is to prove dh(r)/dr0Sincein(25), both g(r)and var(cos2θ)/cos2θ2 are always positive, to achieve our goal, we only need to prove the two theorems below Theorem 21 Q 1(r)≡g(r)−1−2g(r)cos2θ2 0 (26) Theorem 22 Q 2(r)≡var(cos2θ)−1cos2θ 0 (27) Remark 23Question Evaluate The Integral π/2 9 Cos2(θ) Dθ 0 This problem has been solved!

Int 0 Pixsin 6xcos 4x Dx Pi 2int 0 Pisin 6xcos 4x Dx

Evaluate The Integral P 47 9 Cos2 8 Cos2 8 D8 Youtube

Course Title MATH 22A;4 Abstract and Applied Analysis In this study, our goal is to prove dh(r)/dr0Sincein(25), both g(r)and var(cos2θ)/cos2θ2 are always positive, to achieve our goal, we only need to prove the two theorems below Theorem 21 Q 1(r)≡g(r)−1−2g(r)cos2θ2 0 (26) Theorem 22 Q 2(r)≡var(cos2θ)−1cos2θ 0 (27) Remark 23Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history

Solutions Manual For First Course In Differential Equations With Modeling Applications 11th Edition By Mankiw234 Issuu

Solved Example 3 Find Dx Solution Let X 2 Tan 8 Z 2 8 Chegg Com

In Exercises, write the given system of linear equations as a matrix equation of the form Ax = b a x 1 2x2 3x3 = 0 2x1 x2 5x3 = 4 b x1 2x3 = 1 x1 x2 = 2 x2 x3 = 1 View AnswerEvaluate the integralπ/47 9 cos2(θ)cos2(θ) dθ09/03/18 · Mar 9, 18 see below Explanation We have, #cos2theta=cos(thetatheta)# Or,applying #cos(ab)=cosacosbsinasinb#,we see, #cos2theta=costheta xxcosthetasinthetaxxsintheta# = #cos^2theta(1cos^2theta)# {since #cos^2thetasin^2theta=1#} = #2cos^2theta1# {#color(red)("Hence " proved)#} Answer link Related questions How do I

Ex 6 2 9 Prove That Y 4 Sin 2 Cos Theta Is Increasing

Solved Example 1 Evaluate X2 Solution Let X 9 Sin 8 Wh Chegg Com

R 2 1 R \u03c0 2r cos \u03b8 r 2 cos2 \u03b8 d\u03b8 R 2 1 R 3 \u03c02 \u03c0 r cos\u03b8 r 2cos2 \u03b8 d\u03b8 0 b We know R 2 1 r π 2r cos θ r 2 cos2 θ dθ r 2 1 r 3 π2 π School Harvard University;See the answer Evaluate the integral π/2 9 cos 2 (θ) dθ 0 Expert Answer 100% (27 ratings) Previous question Next question Get more help from Chegg Solve it2cos(theta)^2cos(theta)=0 Factor the left side of the equation Tap for more steps Factor out of Tap for more steps Factor out of Multiply by Factor out of Replace the left side with the factored expression Factor out of Tap for more steps Factor out of Raise to the power of Factor out of Factor out of If any individual factor on the left side of the

Trigonometric Integrals

Complex Numbers Trig Identities Ppt Download

9 sin 2θdθ Area = 0 2 π 2 9 = − cos 2θ 4 0 9 = 2 4 r = tan θ, π/6 ≤ θ ≤ π/3 ∫ π 3 1 Area = tan2 θdθ π 2 6∫ π 1 3 = sec2 θ − 1dθ 2 π6 1 √ 1 π π = ( 3− √ − ) 2 6 3 3 1√ 1 3− π = 3 12 11 r = 3 2 cos θ ∫ 1 π Area = 2Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more31/05/10 · from 0 to (π/2) ∫(sin^3⁡θ cos^3⁡θ dθ) Laplace transform May 31, 10 Please type your subject in the School Subject box Any other words, including obscure abbreviations, are likely to delay responses from a teacher who knows that subject well Writeacher May 31, 10 When the sin/cos are in odd powers, use the substitution cosθdθ=d(sinθ), or sinθdθ=d(cosθ

Complex Numbers Trig Identities Ppt Download

Solution Manual For Engineering Mechanics Dynamics 1st Edition By Soutas Little By Issuu

Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreSolutions for AH maths 09 1 (a) f (x)=( 1) − 2)3 f′(x)=(x − 2)3 3(x 1)(x − 2)2 1 =(x − 2)2 ((x − 2)3(x 1))=(x − 2)2 (4x 1) 1= 0 when x = 2 and when x =− 1 4 1 (b) Method 1 x2 y x = y − 5 ⇒ x2 xy = y2 − 5y 1 2x x dy dx y = 2y dy dx − 5 dy dx 2E1 6 3 dy dx − 1 =−2 dy dx − 5 dy dx 5 =−10 dy dx ⇒ dy dx = −1 2 1 Note a candidate maySolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

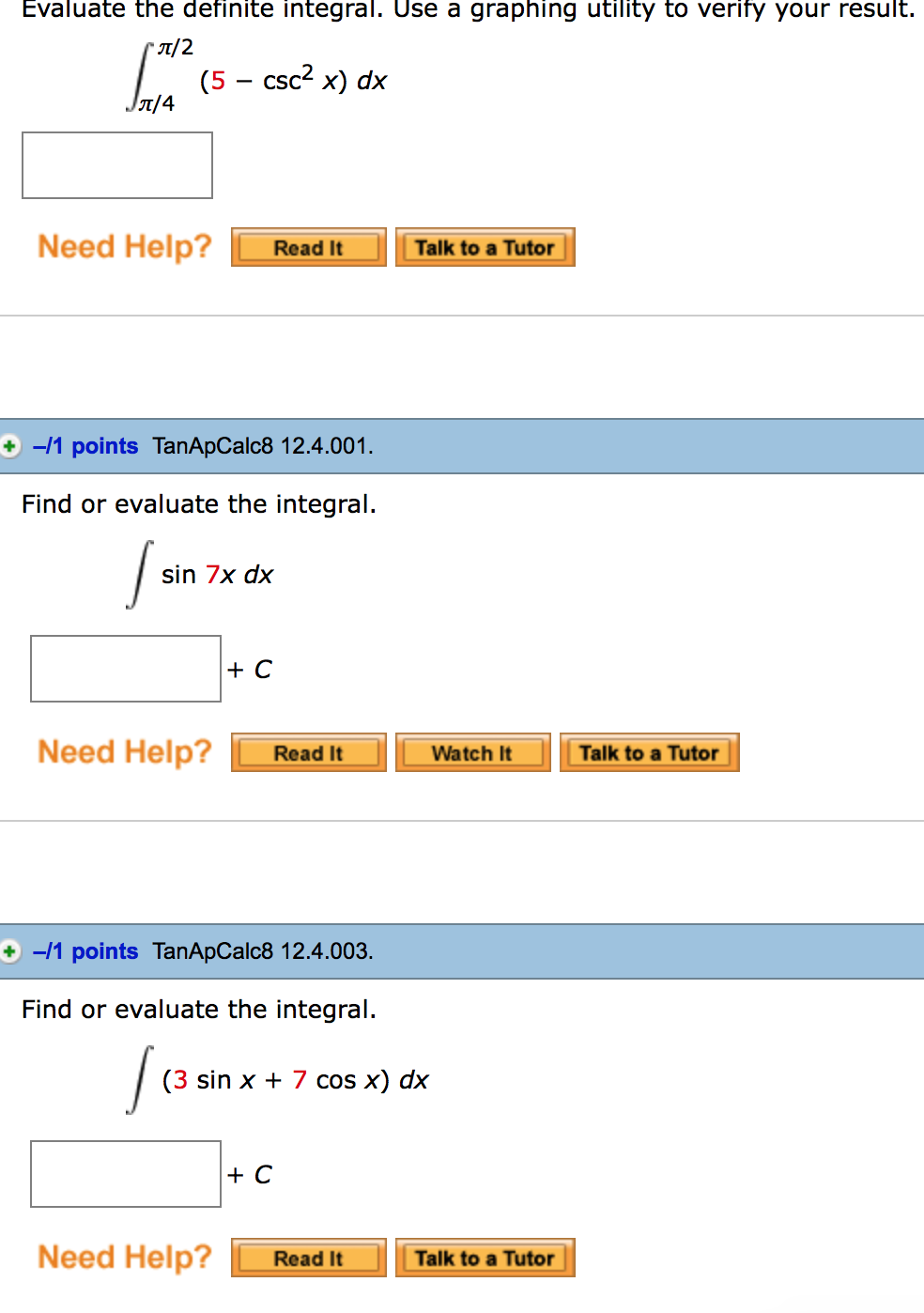
Solved Evaluate The Definite Integral Use A Graphing Uti Chegg Com

Polar Curves Intersections Ppt Download

Given sinθ=076, find θ in degrees to the nearest tenth Maths If sinθ = (square root) 3/2 , find the value of θ in degrees (0 θ ;= π/2 n = 0 Here the values have been found directly for n = 0 and n = 1 Therefore, 6 64 642 A 7 = A 5 = A 3 = A 1 = 16/35 7 75 753 Part II(30 points) Problem 1(15 points) This problem sketches a systematic method for finding antiderivatives of expressions F (sin(θ), cos(θ)), where F is a fraction of polynomials (a)(8 points) With the substitution tan(θ/2) = z, verify that, 2z 2dz sin4 SEÇÃO 104 ÁREAS E COMPRIMENTOS EM COORDENADAS POLARES 15 Α= 2 π 0 1 2 (3 − cosθ)2 dθ = π 0 9 − 6c os θ cos2 θ dθ = 9θ − 6sen θ 1 2 θ 1 4

Solved 81 X Dx Example 1 Evaluate X2 Solution Let X 9 Chegg Com

1 Compute The Following Integral T Ln T Dt

2 sin 2 θ = 2 2 − 2 2 cos2 θ ∫ π 2 π 2sin θ 2 dθ = ∫ π 2 π dθ − ∫ π 2 π cos 2 θdθ 2 π π − sin ¿ ¿ θ − sin 2 θ π π 2 = ¿ θ = π 714 Evalúe la integral dada cambiando a coordenadas polares 7 ∬ D x 2 y dA Donde D es la mitad superior del disco con centro en el origen y radio 5Uploaded By spomoney Pages 10 This preview shows page 7 10 out of 10 pagesDθ = 1 2 żπ 2 π 3 12cosθ ´4(1cos2 θ) dθ = ´3θ 2sinθ ´2sin2θ 2 ˇ ˇ ˇ θ=π 2 θ=π 3 = 1´ π 4 ˝ 以下問題部份小題要用到第七章的觀念，為了題目的完整性一併呈現，但是與第十二章有關的是 (1)(2)(3) 三小題 Problem 7 Let R be the region bounded by the circle r = 1 and outside the lemniscate r2 = ´2cos2θ, and is located on the right

Ex 6 2 9 Prove That Y 4 Sin 2 Cos Theta Is Increasing

Calculus Practice For Dummies Pages 551 600 Flip Pdf Download Fliphtml5

Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreQuestion Evaluate The Integral π/2 3 Cos2θ Dθ 0 This problem has been solved!15/01/12 · Put u = sinΘ so du = cosΘ dΘ Then it reduces to integrating cos^5(u) du For this, use the fact that cos^5(u) = cos(u) (cos²(u))² = cos(u) (1 sin²(u))² = cos(u) (1 2sin²(u) sin^4(u)) Finally, do another substitution v = sin(u) so dv = cos(u) du This results in a polynomial integral ∫ (1 2v² v^4) dv = v (2/3)v^3 v^5/5 C Then go backwards through the two changes

Calculus Practice For Dummies Pages 551 600 Flip Pdf Download Fliphtml5

Unit 4 Applications Of Integration 4a Areas Between Curves

Solution for Evaluate the integral ∫0 π/2 Cos2 θ dθ Social Science AnthropologySolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreSee the answer Evaluate the integral π/2 3 cos 2 θ dθ 0 Videos Stepbystep answer 0150 0 0 Expert Answer 100% (62 ratings) Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculator

Incoming Term: π/2 9 cos 2(θ) dθ 0, evaluate the integral. π/2 9 cos 2(θ) dθ 0, evaluate the integral. π/4 2 + 9 cos2(θ) cos2(θ) dθ 0,